ACTIVIDAD #3

Como resolver un sistema de ecuaciones mediante cramer.

La regla de Cramer es un teorema del álgebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes.
La regla de Cramer es de importancia teórica porque da una expresión explícita para la solución del sistema. Sin embargo, para sistemas de ecuaciones lineales de más de tres ecuaciones su aplicación para la resolución del mismo resulta excesivamente costosa: computacionalmente, es ineficiente para grandes matrices y por ello no es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para matrices pequeñas, particularmente cuando son usadas operaciones SIMD.
Si 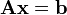es un sistema de ecuaciones. es la matriz de coeficientes del sistema, es el vector columna de las incógnitas y es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:

 

https://www.youtube.com/watch?v=jzIqEehDwp4

La regla de Cramer se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones:

 1  El número de ecuaciones es igual al número de incógnitas.

 2  El determinante de la matriz de los coeficientes es distinto de cero.

Tales sistemas son sistemas compatibles determinados y se denominan sistemas de Cramer.

Sea Δ el determinante de la matriz de coeficientes.

Todo sistema de Cramer tiene una sola solución (es decir, es un sistema compatible determinado) que viene dada por las siguientes expresiones:

 

Δ₁, Δ₂ , Δ₃, ... , Δ_n son los determinantes que se obtiene al sustituir los coeficientes del 2º miembro (los términos independientes) en la 1ª columna, en la 2ª columna, en la 3ª columna y en la enésima columna respectivamente.

 

 

Ejemplo

1